What Is The Range In Math? Unpacking Data's Spread

Understanding what the range in math means can truly help you grasp the variability within any given set of information. It gives you a fast snapshot, sort of like a quick peek, at how much difference exists between the smallest piece of data and the largest one. This concept, you see, is a foundational part of how we look at numbers, especially when we're trying to describe them in a meaningful way. It's not just for statisticians; anyone can use this simple idea to make more sense of the world around them, more or less.

Today, we're going to break down exactly what the range is in math, why it matters, and how incredibly easy it is to figure out. We'll look at some clear examples, just to make sure everything clicks into place for you. By the time we're done, you'll have a solid grip on this key mathematical term, and you'll probably find yourself noticing its relevance in all sorts of places. It's a bit like learning a secret code for data, in a way, that is.

• Longo Lexus El Monte

Table of Contents

• So, What Exactly is "Range" in Math?
  • The Basic Idea: Difference Between Extremes
  • A Look at Data Dispersion
  • Why it Matters for Data Understanding
• How Do You Calculate the Range? Step-by-Step
  • Finding the Highest and Lowest Values
  • Simple Subtraction: The Core Calculation
  • Example Time! Putting It Into Practice
• Range in Different Math Contexts
  • Range in Statistics: A Key Measure
  • Beyond Just Numbers: What Range Tells Us
• Frequently Asked Questions About Math Range
  • How do you find the range of a set of numbers?
  • What is the range used for in statistics?
  • Is range always a positive number?
• Why Understanding Range is Super Helpful
  • Quick Glance at Data Variability
  • Making Sense of Everyday Information

So, What Exactly is "Range" in Math?

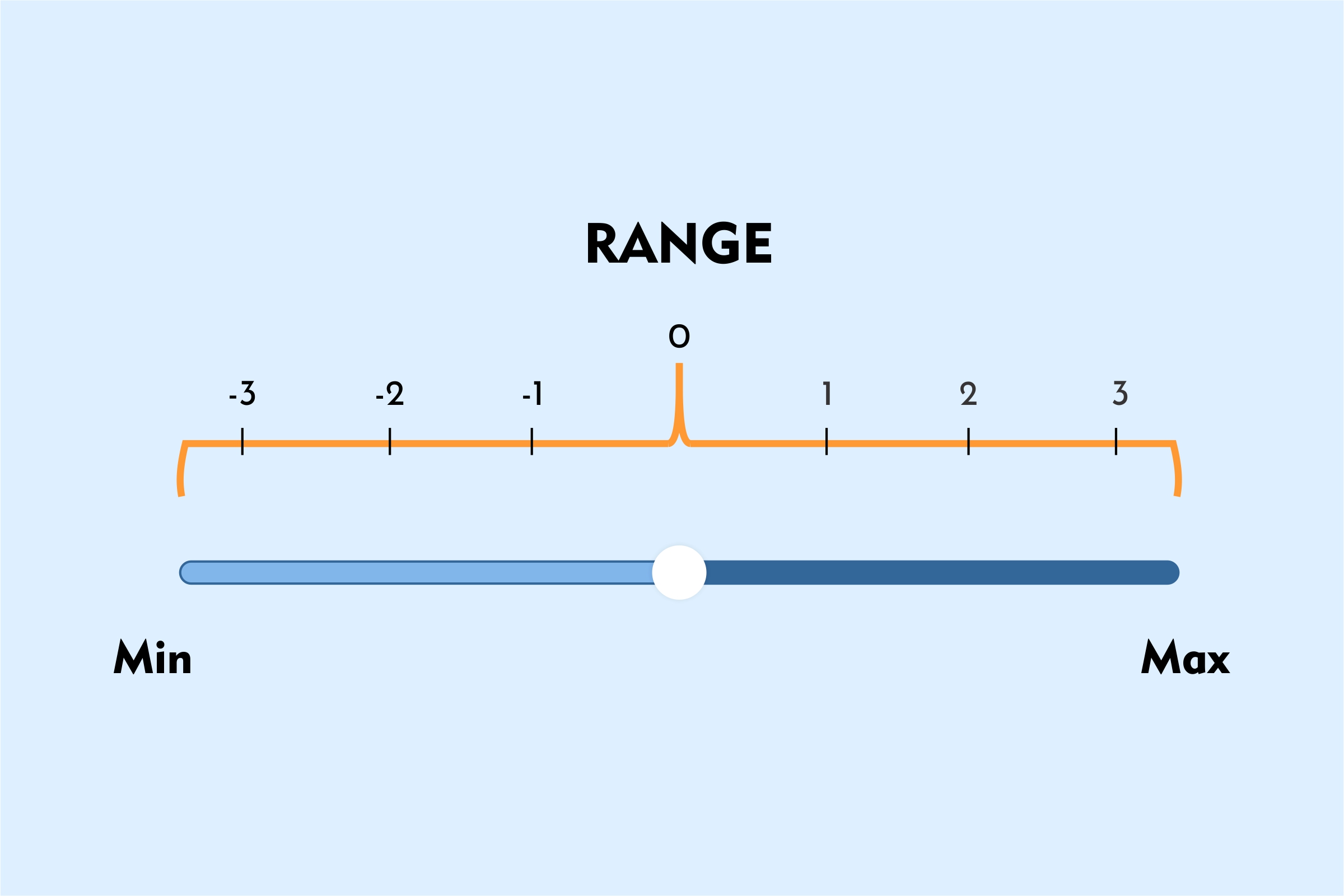
When someone asks, "what is the range in math?" they are typically referring to a statistical measurement. Simply put, the range is the difference between the highest and lowest values in a given set of data. It's a straightforward way to measure dispersion, which is just a fancy word for how much a collection of numbers is stretched out. This measurement, you know, gives us a quick idea of the spread, or variability, within the data, basically.

The Basic Idea: Difference Between Extremes

The core concept of range is incredibly simple. You take the largest number you can find in your data set, and then you subtract the smallest number from it. That's it! That result is your range. For instance, if you have the numbers 4, 6, 9, 3, and 7, the lowest value there is 3, and the highest is 9. The difference between them is 9 minus 3, which equals 6. So, the range for that particular set of numbers is 6. It's pretty direct, isn't it?

This idea of finding the "distance" between the extremes is what makes range so intuitive. It tells you, in a single number, how much ground the data covers from one end to the other. Think of it like measuring the length of a line segment; you're just finding the span. This simple calculation, you know, serves as a quick initial assessment of how much variation is present in your data, more or less.

• What Broadway Shows Will Be Touring In 2025 2026

A Look at Data Dispersion

In math, especially when we're talking about statistics, range is a statistical measurement of dispersion. This means it helps us see how much a given data set is stretched out from its smallest point to its largest point. It's a quick way to gauge the spread of numbers, giving you a sense of how varied or consistent the data might be. For example, a small range suggests the numbers are pretty close together, while a large range indicates they are quite spread out. It's very much about understanding that overall stretch, you see.

Consider two different lists of numbers. One might have values like 10, 11, 12, 13, 14. Its range would be 4. Another list could have 1, 5, 10, 15, 20. Its range would be 19. Even without looking at every number, you can tell that the second list has a much wider spread of values. This immediate insight into dispersion is why range is such a crucial component of every data collection analysis. It really helps you get a feel for things, doesn't it?

Why it Matters for Data Understanding

Understanding the range in math is quite important because it provides a fundamental measure of data variability. It's a simple, straightforward way to get a first impression of how consistent or inconsistent a set of numbers might be. For instance, if you're looking at the daily temperatures in a city, a small range over a week might suggest stable weather, while a large range could mean wild temperature swings. This basic insight helps you make quick judgments about the data. So, it's pretty useful for everyday situations, actually.

The range helps us quickly identify the boundaries of our data. It tells us the "outer limits," so to speak, of the numbers we are working with. This can be particularly helpful when you need to quickly compare two different data sets. If one set has a much larger range than another, you instantly know that its values are more spread out. This immediate understanding of spread is, you know, a very valuable first step in any data exploration, more or less.

How Do You Calculate the Range? Step-by-Step

Calculating the range is one of the simplest statistical operations you can perform. It doesn't require complex formulas or advanced mathematical skills. All you need is your set of numbers, and you're ready to go. The process is quite direct, and once you do it a couple of times, it becomes second nature. It's a bit like finding the tallest and shortest person in a room and then noting the difference in their heights, you know?

Finding the Highest and Lowest Values

The first step in calculating the range is to identify the highest and lowest values within your data set. This might seem obvious, but it's a critical initial point. Sometimes, data sets can be quite long, so you'll need to carefully scan through all the numbers. It often helps to arrange the numbers in order from smallest to largest, though this isn't strictly necessary for finding the range itself. However, it can make spotting the extremes much easier. For example, if your numbers are all mixed up, putting them in order just makes things clearer, doesn't it?

Let's say you have the following test scores: 78, 92, 65, 88, 70, 95, 81. To find the highest and lowest values, you'd scan through them. The highest score you see is 95. The lowest score is 65. These two numbers are the ones you'll use for your calculation. The highest value is sometimes called the largest value, largest number, or maximum value, while the lowest is often called the smallest or minimum value. So, you know, it's pretty straightforward to pick them out, actually.

Simple Subtraction: The Core Calculation

Once you've pinpointed the highest and lowest values in your data set, the next step is just simple subtraction. You take the highest value and subtract the lowest value from it. The result of this subtraction is the range. It's truly that straightforward. This single calculation gives you the full spread of your data. It's a very basic arithmetic step, yet it reveals a lot about the numbers you're working with. It's almost like finding the length of a jump, isn't it?

Using our previous example of test scores (highest 95, lowest 65), the calculation would be: Range = Highest Value - Lowest Value. So, Range = 95 - 65 = 30. This means the test scores span 30 points from the lowest to the highest. This difference tells you how much variation there was in the scores. It's a quick way to summarize the spread, you know, without needing to list every single score, more or less.

Example Time! Putting It Into Practice

Let's walk through a few more examples to make sure the concept of range is crystal clear. Practice really helps solidify these ideas. With this key math vocabulary in mind, you'll see how quickly you can apply it to different situations. We'll use various types of numbers, just to show how versatile this measurement is. It's a rather simple skill, but very useful, you know?

Example 1: Daily Temperatures
Imagine the temperatures in degrees Fahrenheit for a week were: 55, 60, 58, 62, 57, 61, 59. First, identify the highest temperature: 62. Next, identify the lowest temperature: 55. Now, calculate the range: 62 - 55 = 7. So, the range of temperatures for that week was 7 degrees. This tells you the temperature didn't swing wildly, which is pretty good for planning your outfits, isn't it?

Example 2: Number of Books Read
A group of friends read the following number of books in a month: 2, 5, 1, 8, 3, 4. Highest number of books: 8. Lowest number of books: 1. Calculate the range: 8 - 1 = 7. The range of books read is 7. This shows a fairly wide difference in reading habits among the friends. It's quite interesting to see that spread, you know, apparently.

Example 3: Student Heights (in inches)
Consider a small group of students with heights: 60, 68, 63, 71, 65. Highest height: 71 inches. Lowest height: 60 inches. Calculate the range: 71 - 60 = 11. The range of heights is 11 inches. This means there's an 11-inch difference between the tallest and shortest student in this group. It just gives you a sense of the height variation, doesn't it?

As you can see from these examples, the method for finding the range remains consistent regardless of the numbers you are working with. It's always about finding those two extreme values and then simply subtracting the smaller from the larger. This consistency makes it a very reliable and easy-to-use measure. It's almost universally applicable, you know, which is pretty neat.

Range in Different Math Contexts

While we're mostly talking about "range" in the context of statistics, it's worth noting that the word "range" can pop up in other areas of mathematics too, like when discussing functions. However, when people ask "what is the range in math" without further context, they are almost always referring to its statistical definition. Our focus here is on its use as a measure of data variability. It's important to keep that distinction in mind, you know, just so there's no confusion, more or less.

Range in Statistics: A Key Measure

In statistics, range in math is the interval between the two extremes—the highest and lowest values—of the distributed numbers. It represents the difference between the highest and lowest values in a data set, serving as a measure of data variability. This makes it a crucial component of every data collection analysis, as it offers a quick and initial insight into the spread of data. It's often the first measure of dispersion that people learn, and for good reason, you know, it's very simple to grasp, apparently.

While the range is simple to calculate and easy to understand, it's also important to know its limitations. It only uses two values from the entire data set: the maximum and the minimum. This means it doesn't tell us anything about how the other numbers are distributed within that spread. For example, two data sets could have the same range but have their numbers clustered very differently. Still, for a quick overview, it's incredibly useful. It's pretty much a starting point for looking at data, isn't it?

Beyond Just Numbers: What Range Tells Us

The range isn't just a number; it tells a story about the data. A small range suggests that the data points are close together, indicating consistency or uniformity. Think about a class where all students scored very similar grades; the range would be small. This implies a certain level of predictability or stability within that data. It's quite telling, you know, about the overall consistency, basically.

Conversely, a large range indicates that the data points are widely spread out, suggesting variability or inconsistency. Imagine a company where employee salaries vary greatly from the lowest-paid intern to the highest-paid executive; the range would be very large. This signals a broad spectrum of values, which can be important for understanding diversity or disparities within the data. It's a pretty strong indicator of how much things differ, isn't it?

So, the range, while simple, helps us quickly interpret the nature of a data set. It allows for quick comparisons between different sets of data, helping us to immediately see which one has more or less variation. This initial insight is often enough to guide further, more detailed analysis. It really does give you a good first impression of the data's character, you know, and that's rather valuable.

Frequently Asked Questions About Math Range

It's natural to have questions when you're learning new math concepts, even ones as straightforward as range. Here are some common questions people often ask about "what is the range in math," along with clear, simple answers. These questions tend to come up a lot, so addressing them can really help clear things up for you. It's almost like anticipating your thoughts, isn't it?

How do you find the range of a set of numbers?

To find the range of a set of numbers, you follow two easy steps. First, you look through all the numbers in your collection and identify the very highest value and the very lowest value. Then, you simply subtract the lowest value from the highest value. The number you get from that subtraction is the range. For example, if your numbers are 10, 2, 7, 15, 5, the highest is 15 and the lowest is 2. So, the range is 15 minus 2, which equals 13. It's quite simple, you know, to work it out.

What is the range used for in statistics?

In statistics, the range is used as a basic measure of dispersion or spread within a data set. It gives you a quick, initial idea of how much the numbers in a collection vary from each other. It tells you the total distance covered by the data, from its smallest point to its largest point. While it's a simple measure, it's useful for a rapid assessment of variability and for comparing the spread of different data sets. It's basically a first glance at how stretched out the numbers are, you know, in some respects.

Is range always a positive number?

Yes, the range in math, when calculated as the difference between the highest and lowest values, will always be a non-negative number. It can be zero if all the values in the data set are exactly the same (meaning the highest and lowest values are identical). However, it will never be a negative number because you are always subtracting the smaller value from the larger value. The "distance" or "spread" between two points can't be negative, you see. So, it's either zero or a positive value, always, apparently.

Why Understanding Range is Super Helpful

Knowing what the range is and how to calculate it isn't just for math class; it's a skill that can genuinely help you make sense of information in your daily life. It's a tool for quick analysis, allowing you to draw immediate conclusions about the consistency or variability of data without needing to perform complex calculations. This simple concept, you know, really empowers you to look at numbers with a bit more insight, more or less.

Quick Glance at Data Variability

The range provides an instant snapshot of data variability. When you're presented with a new set of numbers, calculating the range is one of the fastest ways to get a feel for how spread out those numbers are. This quick glance can be incredibly valuable for initial assessments. For instance, if you're comparing the prices of similar products at different stores, the range can quickly show you which store has the most consistent pricing or which one has the widest variety of prices. It's a very efficient way to size things up, isn't it?

Imagine you're tracking your daily steps. If your range of steps over a week is very small, it means you're pretty consistent with your activity. But if the range is large, it suggests some days you walked a lot and other days very little. This immediate feedback helps you understand your patterns. It's pretty neat how one number can tell you so much about variation, you know, actually.

Making Sense of Everyday Information

From understanding economic reports to analyzing personal finance, the concept of range is surprisingly applicable. When you hear about the "range of incomes" in a city, you immediately get a sense of the economic disparity. Or, when you look at the "range of scores" on a video game leaderboard, you understand how much difference there is between the top players and those just starting out. It helps you contextualize numbers you encounter every day. This kind of thinking, you know, helps you become a more informed person, basically.

Being able to quickly calculate or even just conceptualize the range of a data set allows you to interpret information more effectively. It's a fundamental building block for understanding more advanced statistical concepts later on, but its immediate utility lies in its simplicity and clarity. So, it's a very practical piece of knowledge to have in your mental toolkit. Learn more about basic math concepts on our site, and link to this page for more on statistics basics. It's pretty much a gateway to deeper understanding, isn't it?

Remember, the range is just one way to look at data, but it's a powerful one because of its ease of use. As of July 29, 2024, this simple concept remains a cornerstone for anyone beginning to explore numbers and their stories. It helps you get a quick feel for how much "stretch" there is in any collection of figures you might come across. It's a bit like measuring the full span of something, you know, very directly.